A newtoni törvények
A fizika a matematikához hasonlóan azaxiomatikus
bizonyítás módszerét alkalmazza. Ennek működési
elve, hogy minden állításhoz megkeressükazt az
alaptételt, amelynek alapján levezethető. Az alapokatkeresve
végüleljutunk ahhoz a tételhez, amely továbbmár
nem egyszerűsíthető, és annyira nyilvánvaló,hogy
további bizonyítást nem igényel. Az ilyenalaptételt
axiómának nevezzük. Az axiómákelső megfogalmazása
a geometriára vonatkozóan Euklidésztől(Eukleidész,
Kr.e. III. század, Alexandria) származik.
Isaac Newton (1643-1727, Opera quae extant omnia, commentariis
illustrabat; Philosophiae naturalis principia mathematica; Optics or a treatise
of the reflections, refractions, inflections and colours of light, also two
treatises of the species and magnitude of curvilinear figures) alaptörvényeit
is axiómáknak nevezzük
A newtoni axiómák leírásánál
a testeket kiterjedés nélküli anyagi pontoknak tekintjük.
Tömegük ennél fogva van, de az egyetlen pontban összpontosul.
I. A tehetetlenség törvénye (Galilei és Kepler
törvényei alapján)
Minden test megmarad a nyugalom(vagy
az egyenes vonalú egyenletes mozgás) állapotában,
míg más testek hatása mozgásállapotának
megváltoztatására nem készteti.
Ez tehát a legegyszerűbb mozgás. A vonatkoztatási
rendszert, amelyben létrejöhet, inerciarendszernek nevezzük.
Következtetések és megjegyzések:
Dinamikai eszközökkel nem különböztethető
meg egymástól a nyugalom és az egyenes vonalú
egyenletes mozgás. Erre a kinematika eszköztára alkalmas,
a megállapítás eredménye függ a vonatkoztatási
rendszertől, t.i., hogy együtt mozog-e a megfigyelt testtel.
Ha a vonatkoztatási rendszer is és a megfigyelt
test is gyorsuló mozgást végez, az egymáshozviszonyított
mozgásuk kinematikai eszközökkel nemfigyelhető meg, de dinamikai
módszerekkel észlelhető (de ezmár a második axióma).
Ha azt mondjuk, hogy körmozgásnál
az állandó szögsebességű mozgás analóg
az egyenes vonalú egyenletes mozgással, akkor az első axiómára
vonatkozóan téves következtetésre jutunk. Például
a Hold körmozgása állandó irányú
ésállandó szögsebességű mozgás. De,
ha eztváltozatlan mozgásállapotnak tekintjük, elfelejtkeztünk
arról, hogy a Hold sebességének iránya folytonosan
változik; méghozzá a Föld hatására.
Az első axióma nem nevezi nevén sem a mozgásállapot
megváltozását, sem a más testek hatását.
A második axióma feladata néven nevezni ezeket a fizikai
mennyiségeket.
II. Erő és tömeg
Egy pontszerű test a gyorsulása
egyenesen arányosa testre ható (a gyorsulással azonos
irányú) F erővel, és fordítva arányos
a test m tömegével.
Megneveztük tehát az első axiómában
szereplő mennyiségeket. A mozgásállapot megváltozásának
neve: gyorsulás. A más testek hatásátettől
kezdve erőnek nevezzük. Természetesen későbbmegismerünk
majd más erőket is: nyomóerőt (hidrosztatika),húzóerőt
(szilárdságtan), elektrosztatikus erőt(villamosságtan),
stb. A felsorolt fizikai jelenségeket kölcsönhatásoknak
nevezzük. Mindegyikhez tartozik egy olyan tehetetlenség-jellegű
mennyiség, amely kifejezi a testek azon tulajdonságát,
hogy véges képességük van a mozgásállapot
megváltoztatására. Ez most itt a tömeg:
atestek tehetetlenségének mértéke.
Alkalmazás: a dinamikai tömegmérés.
Abból indulunk ki, hogy a tömeg (korlátos feltételekkel)
állandó. F = m
1a
1 = m
2a
2. Rezgőmozgást létrehozva
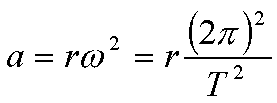
,ezért
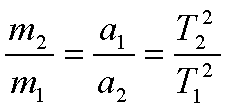
Tömegmegmaradás törvénye (Lomonoszov és
Lavoisier törvényeivel megerősítve)
A tömeg additív, ezért
skalár. A tömegek összege akkor is állandó,
ha a test halmazállapota megváltozik, vagy kémiai átalakulások
játszódnak le.
Következtetések és megjegyzések
Később azokat a fizikai mennyiségeket,
amelyek additívak, extenzíveknek fogjuk nevezni. Ilyen
a tömeg is (a hőtanban ilyen lesz a hőmennyiség).
A II. axiómánál láttuk,hogy
a tömeg skaláris mennyiség. Láttuk u.i. abból,
hogy a gyorsulás irányát az erő határozza meg;
a tömeg nem befolyásolja. Szorzatuk tehát vektornak skalárral
való szorzata.
Ötven évvel Newton után (Lomonoszov
és Lavoisier korában) még bizonyításra
szorult például az, hogy a gázok éppoly anyagok,
mint a cseppfolyós és a szilárd testek. A kémia
vonatkozásában a fenti törvény a tömeghatás
törvényében nyert megfogalmazást.
A XX. században az atomrombolás felfedezésével
ismertek fel egy olyan jelenséget, amely nem felel meg az anyagmegmaradás
törvényének. Ez a magreakciók tömegdefektusa.
Így újabban szokásos ezt a tömeg- és energiamegmaradás
(együttes) törvényének nevezni.
További megfontolást igényel, hogy
van két fizikai jelenség, amely hatásában azonos,
mégis van közöttük különbség. Ezért
beszélünk tehetelen tömegről és súlyos
tömegről. A nagy fizikai laboratóriumok Einstein óta
kísérleteznek annak kísérleti bizonyításával,
hogy ezek azonosak-e (vagy különbözőek). A jelentős eltérés
a két fizikai jelenség között abból származik,
hogy a súlyerő nyugalmi állapotban vizsgálható,
míg a gyorsítóerő megjelenéséhez a mozgásállapotot
meg kell változtatni. Mai tudásunkalapján nincs
okunk feltételezni, hogy a súlyos tömeg és a tehetlen
tömeg nem azonos - hacsak meg nem közelítjük a relativisztikus
sebességeket.
Alkalmazás: a statikai mérlegelés.
Ha egy csigán kötelet vetünk át, és mindkét
végére serpenyőt erősítünk, akkor ez a rendszer
nyugalomban fog maradni, ha mindkét serpenyőbe azonos súlyt
helyezünk. Az egyik a mérendő súly, a másik egy
alkalmasan megválasztott mérlegsúly. Éppígy
statikai egyensúly jön létre, ha egy rugóra felfüggesztjük
a mérendő súlyt, majd a mérlegsúlyt. A rugó
két különböző megnyúlásának hányadosa
a két súly hányadosával azonos (ha mérés
közben a rugó tényleg nyugalomban volt. Ennek figyelmen
kívül hagyása még ma is lehetővé teszi a
mérlegeléseknél való visszaéléseket!).
A XIX. században nem voltak még ismeretesek
az anyagok súlyára és tömegére vonatkozó
adatok. Mivel a kilogram mértékegységet az egy köbdeciméter
víz térfogata alapján definiálták, s annak
sűrűségét állandónak vélték, félreérthetővé
váltak a mértékegységek. Ezért száz
éven át érvényes volt, hogy 1,000 028dm3
= 1 liter. A XLV. mérésügyi törvény
(1991) óta a két mértékegységet újra
azonosnakkell tekintenünk!
III. a kölcsönhatás törvénye (akció-reakció
törvénye)
Ha egy testre egy másik
F erővel hat, akkor amásik testre az egyik ugyanekkora erővelhat.
Az erők hatásvonala természetesen egybeesik; azonos nagyságúak,
de ellenkező irányúak.
Habár a Nap tömege 330 000-szer nagyobba
Föld tömegénél, mégis ugyanakkora erővelvonzza
a Földet, mint a Föld a Napot.
IV. Az erőhatások függetlenségének elve
Ha egy anyagi pontra több erő
hat, akkor hatásuk azonos az eredőjükkel jellemzett egy erő hatásával
Ha az eredő értéke nulla, akkor a test egyensúlyban van.
Ebben a törvényben fogalmazhatunk meg először
erőket úgy, hogy irányuk egymáshoz képest a térben
bármely tetszőleges irányt felvehet.