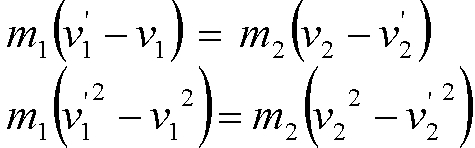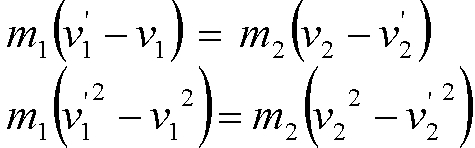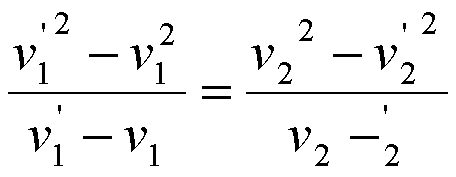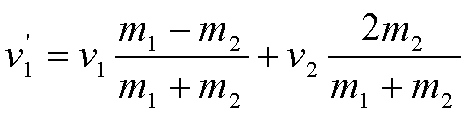A rugalmas ütközésről
m1 és m2 tömegek ütköznek. Ütközés előtti sebességük
v1 és v2. Ütközés utáni sebességük v1'
és v2'.
Az impulzus (súlypont) megmaradásának tétele:
m1v1'+m2v2 '=m1v1+m2v2
A kinetikai energiák megmaradásának tétele:
1/2m1v1'2+1/2m 2v2'2=1/2m1v12
+1/2m2v22
Az együtthatókkal egyszerűsítünk:
m1v1'2+m2 v2'2=m1v12+m
2 v22
Rendezzük a tömegeket az egyenlet azonos oldalára:
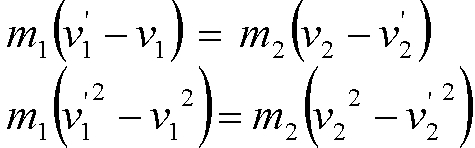 Ha elosztjuk az egyenletek baloldalait egymással és jobboldalait is egymással,
akkor az egyenlőség érvényes marad (bizonyos peremfeltételekkel, pl. egyik
tömeg sem nulla nagyságú):
Ha elosztjuk az egyenletek baloldalait egymással és jobboldalait is egymással,
akkor az egyenlőség érvényes marad (bizonyos peremfeltételekkel, pl. egyik
tömeg sem nulla nagyságú):
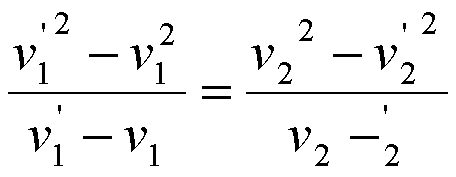 A számlálókban nevezetes szorzat található (két szám összegének és különbségének
szorzata). Elvégezve az egyszerűsítést:
v1'+v1=v2+v2'
Ezt m2-vel megszorozva, majd m2v2'-t kifejezve
kapjuk:
m2v2'=m2v1'+m2v1-m2v2
Ugyanígy, a mozgásmennyiségekre vonatkozó egyenlőségből:
m2v2'=m1v1+m2v2-m1v1'
A két kifejezést egyenlővé tesszük egymással:
m2v1'+m2v1-m2v2=m2v2'=m1v1+m2v2-m1v1'
Minthogy az 1-es jelű testnek az ütközés utáni sebessége érdekel bennünket,
v1' szerint rendezzük az egyenletet:
m1v1'+m2v1'=m1v1-m2v1+m2v2+m2v2
Kiemelve a sebességeket:
v1'(m1+m2)=v1(m1-m2)+v22m2
Végülis v1':
A számlálókban nevezetes szorzat található (két szám összegének és különbségének
szorzata). Elvégezve az egyszerűsítést:
v1'+v1=v2+v2'
Ezt m2-vel megszorozva, majd m2v2'-t kifejezve
kapjuk:
m2v2'=m2v1'+m2v1-m2v2
Ugyanígy, a mozgásmennyiségekre vonatkozó egyenlőségből:
m2v2'=m1v1+m2v2-m1v1'
A két kifejezést egyenlővé tesszük egymással:
m2v1'+m2v1-m2v2=m2v2'=m1v1+m2v2-m1v1'
Minthogy az 1-es jelű testnek az ütközés utáni sebessége érdekel bennünket,
v1' szerint rendezzük az egyenletet:
m1v1'+m2v1'=m1v1-m2v1+m2v2+m2v2
Kiemelve a sebességeket:
v1'(m1+m2)=v1(m1-m2)+v22m2
Végülis v1':
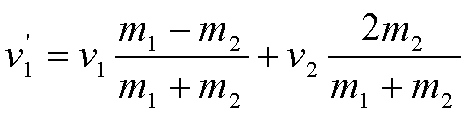 Ha például a két tömeg nagysága megegyező, az első tag kiesik; azaz az
1-es tömeg a 2-es tömeg sebességét veszi fel. Másszóval: a sebességeik
kicserélődnek.
Ha például a két tömeg nagysága megegyező, az első tag kiesik; azaz az
1-es tömeg a 2-es tömeg sebességét veszi fel. Másszóval: a sebességeik
kicserélődnek.
Ha például v2=0 és m2=végtelen (merev falba való
ütközés), akkor a második tag esik ki, és v1'=-v1,
tehát ütközés után az 1-es tömeg ellentétes irányú, de azonos nagyságú
sebességgel mozog.
(Gaspard-Gustave de Coriolis: Théorie mathématique des effects
du jeu de billard, Paris, 1835.)