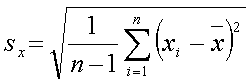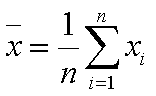Metrológiai tájékoztató fizikából

A következőkben a mérések kiértékelésének metodikájával fogunk foglalkozni
Valódi érték; várható érték. Bármely fizikai mennyiség valódi értéke az ismeretelmélet korlátaival jellemezve, nem ismerhető meg. Ennek a ténynek az egyik legismertebb vonása az, hogy minden mérőeszköz, mérési eljárás beavatkozást jelent a vizsgált objektum tulajdonságaiba, tehát valamilyen fokon módosítja azt. Például a villamos feszültségmérő söntöli a mért áramkört, és ezáltal meghamisítja magát a megismerni kívánt mennyiséget.
Helyes érték. A helyes érték a valódi értéknek lehető legjobb műszaki becslése.
Mért érték. A mért érték a helyes érték meghatározása céljából végzett méréssorozat egy-egy eleme. A mérési eljárás lényege, hogy a mért értékek halmazából a helyes értékre következtetünk. A leggyakoribb esetben a következtetés módja a számtani középérték (átlag) kiszámítása.
Hiba. hiba = helyes érték - mért érték. Ennek értelmében pozitív a hiba, ha a mért érték kisebb, mint a helyes érték. Minden egyes mért értékhez tarozik egy-egy hiba.
Korrekció. korrekció = helyes érték - mért érték. Ennek értelmében a korrekció a hibával mindíg azonos nagyságú, és ellentétes előjelű. Nagyságát általában csak akkor tudjuk becsülni, ha valamilyen módon ismerjük a hibát okozó jelenségek valamelyikét.
Relatív hiba. relatív hiba = hiba / mért érték. Szokásos százalék mértékegységben is kifejezni. Helyette igen gyakran azt a mennyiséget használjuk, amelyet a hibának a helyes értékkel való osztásából kapunk.
Pontosság. A pontosság a hiba inverze. Sokszor a relatív hiba inverzét célszerű használni. A gyakorlatban sűrűn előforduló tévedés, hogy a relatív hibát pontosságnak nevezik, holott az annak épp a reciproka.
Mérési adatok halmazának illeszkedésének vizsgálata esetén minden egyes elemnél értelmezzük a várható értéket és a megfigyelt értéket. Ilyenkor a várható érték valamilyen függvénykapcsolatból származik; értékét tetszőleges pontossággal ismerjük, de a megfigyelt értéktől valamilyen mértékben eltér.

A hibát okozó tényezők két típusba tartoznak.

Rendszeres hiba. A rendszeres hiba nagysága és előjele megismerhető. Meghatározásának lehetőségei: pontosabb mérés, hitelesítés, interpolálás (nóniusz), a parallaxis hiba kiküszöbölése (tüköralátét). A hitelesítést olyan műszerrel kell végeznünk, amely az alkalmazott műszernél kisebb hibával rendelkezik.
Vélelen hiba. Véletlen hiba az az érték, amelynek sem nagyságát, sem előjelét nem ismerjük. A véletlen hiba nértéke nem jósolható meg előre; utólag sem állapítható meg, és véletlenszerű ingadozást mutat. A véletlen hibát kiküszöbölni nem lehet, de a hatása csökkenthető a mérések számának növelésével. A véletlen hiba nagyságának becslésére valók a matematikai statisztikai, biometriai eljárások.
A jelenségek közötti kapcsolat - igen hasonlóan a hibák két típusához - kétféle lehet.
Kauzális, okozati kapcsolat. Ha két esemény között okozati összefüggés van, akkor az első esemény alapján korlátlan biztonsággal megjósolható a másik esemény létrejötte; a második esemény létrejöttének valószínűsége p=1, azaz 100 %. Az okozati összefüggés rendszeres hibát hoz létre.
Sztochasztikus, valószínűségi, véletlen esemény. Ha egy esemény következtében egy másik esemény bizonytalan mértékben jön létre, akkor véletlen eseményről beszélünk. Például; egy dobókockának hat oldala van. Ezért 1/6-od a valószínűsége annak, hogy épp hatost dobunk. De, ha kipróbáljuk, akkor ez egyáltalán nem teljesül. Ha mondjuk valaki hatszor dob egymás után, és azt várja, hogy a dobások között biztosan egyszer elő fog fordulni a hatos, akkor bizony nagyot fog tévedni. Mert lehet, hogy többször is hatost dob, de az is lehet, hogy ez csak huszadszorra sikerül.
Vegyük példaképpen a ferde hajítás esetét. Ha a ferde hajítás képleteivel kiszámítjuk az eldobott kő becsapódási helyét - figyelembe véve a levegő fékező hatását és a Föld görbületét - akkor biztosan tudjuk, hol fog lehullani a kő. Ha viszont a valóságban végezzük el a kísérletet, azt fogjuk találni, hogy egy nehezen meghatározható körön belül lesznek a találatok, nem pontosan a kiszámított helyen. Természetesen. Hiszen a levegő sohasem nyugodt, mindíg van valamekkora kiszámíthatatlan mértékű és irányú mozgása. A mikrogravitációs jelenségek meg a Föld görbületéből számított hatást fogják kiszámíthatatlanná tenni. Hát még, ha az eldobott kő alaktalan; repülés közben forog; és ezáltal kiszámíthatatlanul változó közegellenállás fog rá hatni.

A mért értékek típusa

A mért értékek lehetnek folytonos értékkészletűek, de lehet az is, hogy csak megkülönböztetett (diszkrét) értékeket vehetnek fel. Persze, a műszereink nem képesek hiánytalanul leképezni a folytonos értékkészletű számokat. Tegyük fel például, hogy egy villamos feszültségmérőn tíz voltonkénti beosztás van. Tételezzük fel azt is, hogy a mutató a százhuszas beosztás közelében van. Tehát biztos, hogy száztíz voltnál magosabb a feszültség, de az is biztos, hogy százharminc voltnál alacsonyabb. Ilyen esetben a mért értéket százhúsz voltnak tekintjük, bár tudjuk, hogy nem pontosan annyi. Így tehát a folytonos értékkészletű számokat diszkrét értékkészlet formájában ábrázoltuk.
Vannak műszerek, amelyek ezt a műveletet szerkezeti felépítésüknél fogva emberi közreműködés nélkül elvégzik. Ilyenek a digitális mérőműszerek, és az általuk végzett műveletet kvantálásnak nevezzük. A kvantálással tehát folytonos értékkészletű számhalmazt diszkrét számhalmazzá komvertálunk.

A hibák becslésének módszerei

Megbízhatósági intervallum, konfidencia intervallum. Megadhatunk egy számot, amelyre vontatkoztatva igaz az az állítás, hogy a mért érték a helyes értéktől nagyobb mértékben nem fog eltérni adott valószínűségnél jobban, vagy adott gyakoriságnál gyakrabban.
Az első esetet egyedi mérésekre célszerű vonatkoztatni. Például lehet nyolcvan százalék a valószínűsége annak, hogy a málnaszörp sűrűségének valamelyik mérésénél a mért érték és a helyes érték eltérése kisebb lesz, mint 10 kg/m³.
A második esetet célszerű méréssorozatnál értelmezni. Például igen sokszor megmérve a málnaszörp sűrűségét, az esetek nyolcvan százalékában az eltérés kisebb lesz, mint 10 kg/m³. Ez a mérések relatív gyakoriságára vonatkozó megállapítás. A két eset semmiképpen sem lehet azonos, annak ellenére, hogy azonos számértékeket vettünk a példánkhoz.
A megbízhatósági intervallum, konfidencia intervallum tehát a hibák becslésére használható mennyiség.
A helyes érték meghatározására (a véletlenszerű hatások kiküszöbölése céljából) méréssorozatot végzünk, és matematikai eszközök felhasználásával becslést végzünk a helyes értékre vonatkozóan. A legismertebb ilyen becslési mód a számtani közép (az átlag) kiszámítása.

A medián értékének meghatározásához a mért értékeket nagyság szerinti sorrendbe rendezzük. A medián a középső érték lesz, az az érték tehát, amelynél kisebb és nagyobb eredmény egyforma gyakorisággal fordult elő. Előfordulhat, hogy páros számú mérési eredményünk van. Ilyenkor a két középső érték számtani középarányosát választjuk mediánnak.
A módusz a legnagyobb gyakoriságú érték.
Gyakran találkozunk azzal a megállapítással, hogy véletlen hibák esetén az átlag, a medián és a módusz egybeesik. Hozzá kell tennünk: ez csak folytonos értékkészletű, normál eloszlású adathalmaz esetén igaz.
Terjedelem. A nagyság szerint rendezett mérési adathalmaz legnagyobb és legkisebb értékének különbsége (távolsága) a terjedelem. A folytonos értékkészletű, elméleti eloszlástípussal jellemzett sorozatok legnagyobb értéke a végtelen, legkisebb értéke a mínusz végtelen. A valóságos adatok azonban csak egy véges tartományban fordulnak elő, tehát értelmezhető náluk a terjedelem fogalma.
A hiba (pontosabban a megbízhatósági intervallum) nagyságának becslésére leginkább a szórást használjuk; ritkábban az átlagos abszolút eltérést.

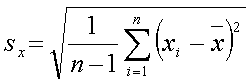
Mérési módszerek áttekintése
Összeállította: dr. Zana János