Az alapvető fénytani felfedezések (pl. fényvisszaverődés) már Euklides feljegyzéseiben is a fény egyenes vonalú terjedésére utaltak. A fénytörést, a színszóródást a XVII. században egyenes vonalban haladó fénysugár segítségével meg is tudták magyarázni. Voltak azonban más jelenségek is, mint a fényinterferencia, fényelhajlás, polarizáció, amelyek csak a fény hullámtermészete alapján értékelhetők. Bár a Huygens-féle hullámelmélettel egyidejűen látott napvilágot a Newton -féle korpuszkuláris elmélet. Ez utóbbi szerint a fény a fényforrásból kirepülő parányi részecskékből áll, amelyek a homogén közegben, az ún. éterben állandó sebességgel mozognak. A maga korában a felismerés igen fontos haladó gondolatot alapozott meg.
Mindegyik leírási mód tartalmazott hiányosságokat. Ezek kiküszöbölését tette lehetővé a Maxwell-féle elektromágneses fényelmélet, a Lorentz-féle elektronelmélet és a Planck-féle kvantumelmélet. Így a fény elektromágneses hullám, amely kvantumokban, ún. fotonokban továbbít energiát. A fény és anyag kölcsönhatásban a fény nem hullámtermészetű, hanem ott szerepet a h energiájú, fénysebességgel haladó fotonok játszanak. A fény e kettős természetét mai ismereteink szerint a kvantum-elektrodinamika tárgyalja matematikai szempontból ellentmondás mentesen.
A geometriai optika a fénysugarat egyetlen vonalnak tekinti, és a jelenségek tárgyalásánál sem a hullámoptikai, sem a korpuszkuláris tulajdonságot nem veszi figyelembe. Az optikai jelenségek szolgálnak alapul a fény optikai sajátosságainak megállapítására. Mi az egyenesvonalú terjedésből következő árnyékjelenségekkel, a fény terjedési sebességével, az optikai eszközökkel és a képalkotással nem foglalkozunk, azt a középiskolai tanulmányok alapján ismertnek tekintjük.
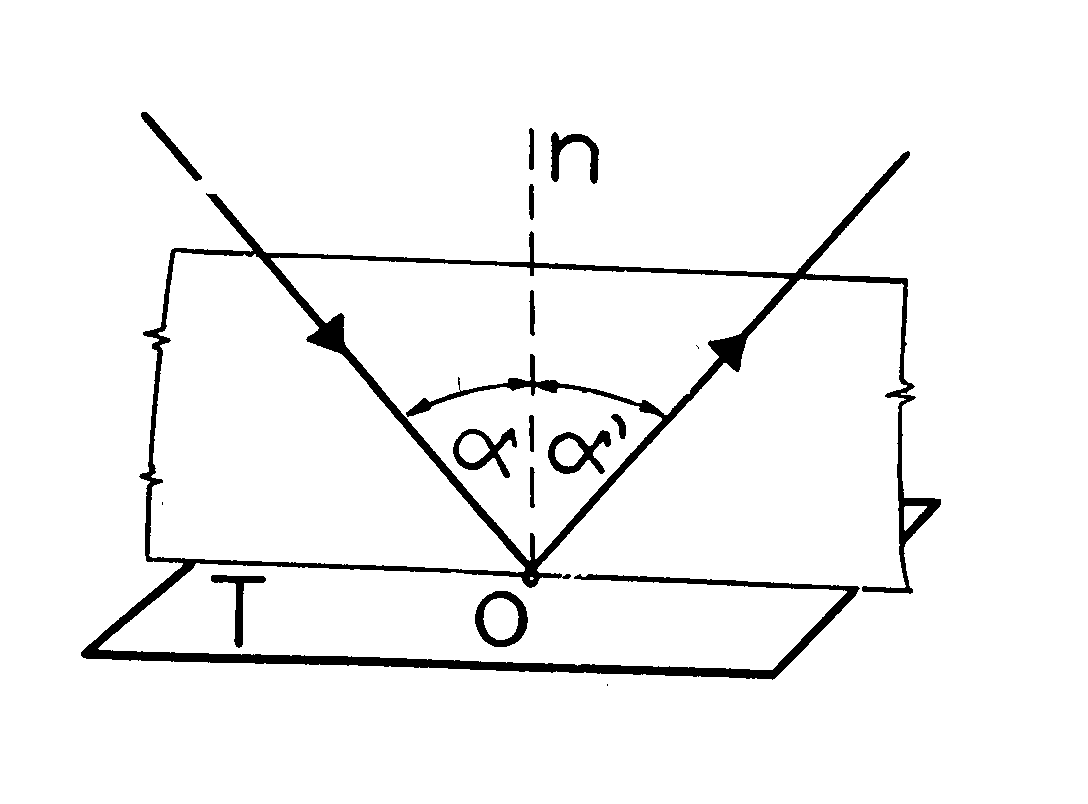
Az anyagok határfelületére érkező fény egy része visszaverődik (reflexió), másik része az anyagba hatolva ott abszorbeálódik, illetve irányváltoztatással, ún. fénytöréssel (refrakció) halad tovább. A visszaverődés lehet tökéletesen szabályos, diffúz, és vegyes. A tökéletesen szabályos visszaverődés jellemzője, hogy a beeső és visszavert fénysugár egy síkban van, és a beesés és visszaverődés szöge megegyezik. (39. ábra)
39. ábra .Tökéletesen szabályos visszaverődés
Az anyagok általában a fényt minden irányban szinte egyenletesen verik vissza. Ez a szórt vagy diffúz fényvisszaverődés teszi lehetővé a minden irányból való láthatóságot. Így a visszaverődés az anyagok jellemzője is. A visszavert és beeső fényáram hányadosa méri a visszaverő- vagy reflexióképességet.
A reflexiós tényező tehát anyagjellemző. Természetesen hasonló mondható el az áteresztő vagy transzmisszió-képességről is.
A fényáteresztés (transzmisszió) szorosan összefügg a fénytörés jelenségével. A fénytörésre érvényes Snellius–-Descartes-törvénye. A megtört fénysugár is a beesési síkban van és a beesési illetve törési szög szinuszának hányadosa az anyagra jellemző állandó.
(40. ábra)
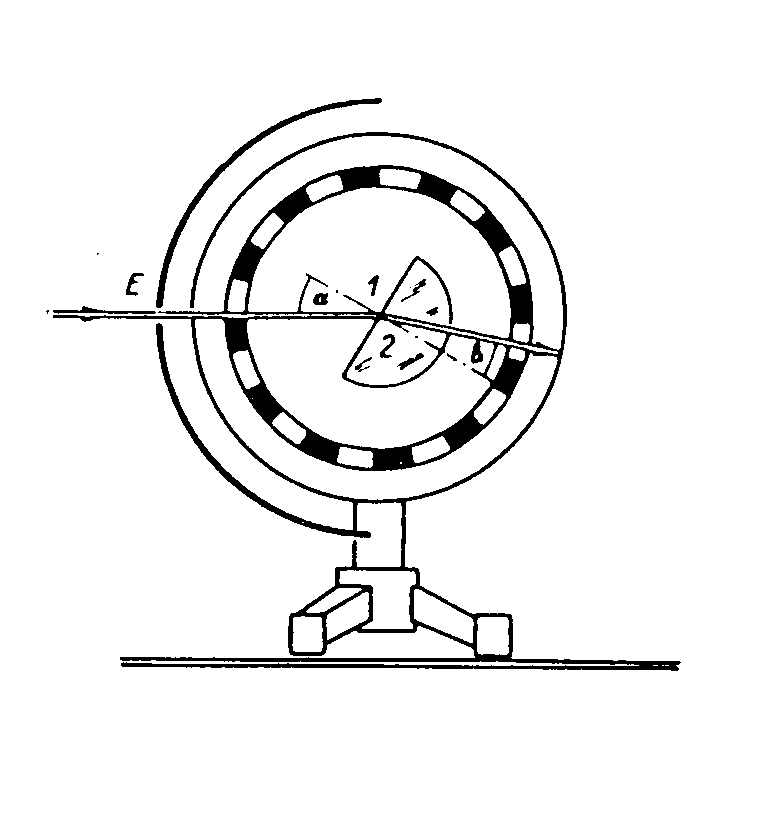
40. ábra. A fénytörés kísérleti szemléltetése
Az n21 a második közeg elsőre vonatkozó törésmutatója. A fénysugár útját megfordítva:
A hullámtanból ismert Huygens elv alapján tudjuk:
(c a vákuumban, cl és c2 a közegben a fény terjedési sebessége)
Az
szorzatot
numerikus apertúrának nevezzük és, mint látható, a fénytörésnél ez állandó.
A korábban említett anyagra jellemző visszaverő és áteresztő képesség a törésmutatókkal kifejezve:
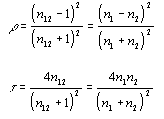
(pl. levegő-víz esetén ró= 2 %, tau= 98 %)
Igen fontos élelmiszerfizikai méréstechnikai jelentősége van a fénytörés azon speciális esetének, amikor a törési szög 90°. Ez a teljes visszaverődés vagy totális reflexió esete. (41. ábra)
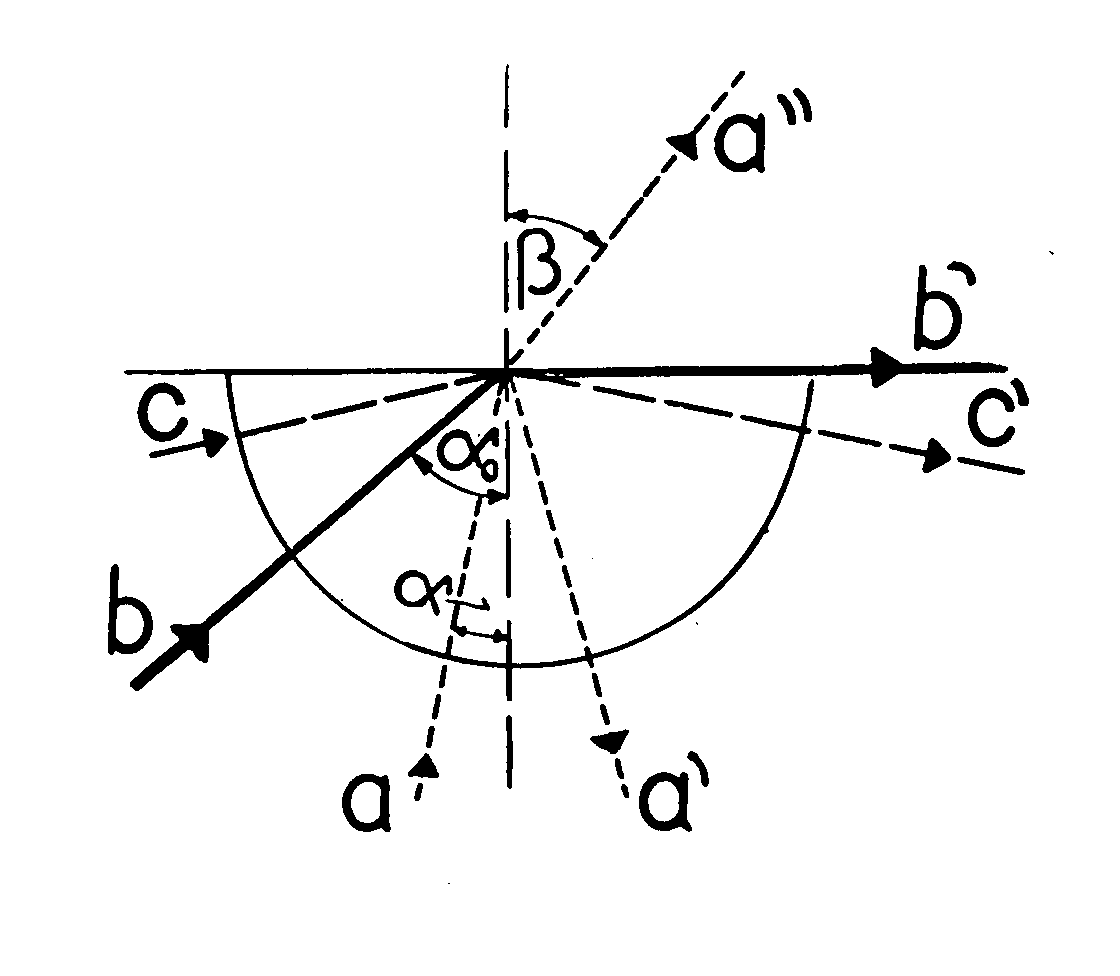
41. ábra. Refrakció és reflexió
(A "2"-es közeg optikai szempontból ritkább). Például víz és levegő esetén alfa0 = 48,5°.
Vissza a kezdőlapra Előző fejezet Vissza a tartalomjegyzékre Ugrás a következő fejezetre